Простые бинарные деревья на Haskell

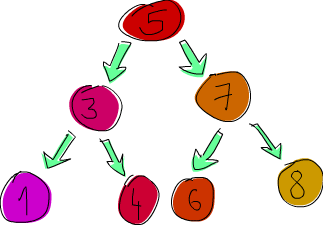
1. Бинарные деревья - очень крутая штука, применяющаяся просто везде: для представления множеств, поиска и т.д. Его полезность в том, что количество операций для поиска элемента пропорционально логарифму количества всех элементов. Все элементы с ключами, большими текущего элемента, находятся в правой ветви, а меньшие - в левой. Рассмотрим простые несбалансированные деревья. Определяется дерево очень просто: дерево либо пусто, либо содержит элемент некоторого типа и из него растут еще два дерева - левое и правое поддерево. Такое рекурсивное определение как нельзя лучше подходит для реализации на нашем любимом Haskell.

data Tree a = EmptyTree | Node a (Tree a) (Tree a) deriving (Show, Read, Eq)

2. Теперь создадим функцию, которая добавляет элемент в дерево. Она должна делать так:

• Если дерево пусто, то мы создаем вместо него синглетон, т.е. дерево с элементом и двумя пустыми поддеревьями.
• Если не пусто, то если элемент меньше текущего, мы добавляем его в левое поддерево, если больше, то в правое. Если элемент совпадает, нужно оставить все как есть.

Как всегда, алгоритм на Haskell реализуется легкой формализацией словесного описания:

singleton :: a -> Tree a  
singleton x = Node x EmptyTree EmptyTree  
  
treeInsert :: (Ord a) => a -> Tree a -> Tree a  
treeInsert x EmptyTree = singleton x  
treeInsert x (Node a left right)   
    | x == a = Node x left right  
    | x < a  = Node a (treeInsert x left) right  
    | x > a  = Node a left (treeInsert x right)  

3. Поиск элемента в дереве тоже более чем прост благодаря его упорядоченной организации:

• Если дерево пусто, то, очевидно, в нем нет искомого элемента
• Если не пусто, то либо мы нашли, что искали, либо если искомое меньше текущего, то ищем в левом поддереве, иначе - в правом.

treeElem :: (Ord a) => a -> Tree a -> Bool
treeElem x EmptyTree = False
treeElem x (Node a left right) 
    | x == a = True
    | x < a  = treeElem x left
    | x > a  = treeElem x right  

4. Преобразование списка в дерево. Можно просто добавить список к пустому дереву, а перед этим реализовать функцию добавления к дереву списка объектов того же типа, что и в вершинах дерева.

makeTree :: Ord a => [a] -> Tree a
makeTree xs = treeListInsert xs EmptyTree

treeListInsert :: Ord a => [a] -> Tree a -> Tree a
treeListInsert [] tree = tree
treeListInsert (x:xs) tree = treeListInsert xs (treeInsert x tree)

5. Преобразование дерева в список также очевидно, причем список получается упорядоченным:

treeToList :: Ord a => Tree a -> [a]
treeToList EmptyTree = []
treeToList (Node a left right) = treeToList left ++ [a] ++ treeToList                            С                                                               right

6. Осталось реализовать: delete element; проверка балансировки... кроме этого, нужно реализовать сбалансированные деревья. так же интересно это сделать параллельно с модулем на языке С